Bentuk umum Persamaan Kuadrat :
Persamaan kuadrat merupakan suatu bentuk persamaan (menggunakan tanda sama dengan "=") dimana pangkat tertinggi dari variabelnya adalah 2.
Variabel merupakan bilangan yang belum pasti nilainya, dan biasanya disimbolkan dengan huruf (contoh: x, y, dan lainnya).
Koefisien adalah suatu bilangan/konstanta yang melekat pada variabel, biasanya dituliskan didepan variabel, sebagai bentuk perkalian.
Karena kuadrat (pangkat dua), maka penyelesaian dari persamaan kuadrat juga ada 2 buah nilai x.
Contoh 1
Tentukan himpunan penyelesaian persamaan kuadrat
Penyelesaian:
Contoh 2
Tentukan himpunan penyelesaian persamaan kuadrat
Penyelesaian:
Contoh 3
Tentukan himpunan penyelesaian persamaan kuadrat
Penyelesaian:
Dari contoh di atas, kita dapat menyelesaikan persamaan kuadrat:
Bilangan yang di dalam akar sering disebut sebagai Diskriminan (D).
Untuk lebih jelasnya, lihat video tutorial tentang penyelesaian persamaan kuadrat klik disini
Sifat-sifat Akar Persamaan Kuadrat
Perhatikan contoh berikut:
Contoh 1
Tentukan akar dari persamaan kuadrat
Penyelesaian:
Contoh 2
Tentukan akar dari persamaan kuadrat
Penyelesaian:
Contoh 3
Tentukan akar dari persamaan kuadrat
Penyelesaian:
Jadi tidak memiliki akar-akar yang riil/nyata (disebut akar imajiner)
Dari ketiga contoh di atas, dapat terlihat bahwa, akar-akar persamaan kuadrat sangat bergantung pada bilangan bulat yang ada di dalam akar (D)
1. Untuk
2. Untuk  , maka persamaan kuadrat memiliki aka-akar yang riil dan kembar.
, maka persamaan kuadrat memiliki aka-akar yang riil dan kembar.
3. Untuk , maka persamaan kuadrat memiliki akar-akar yang tidak riil (imajiner)
, maka persamaan kuadrat memiliki akar-akar yang tidak riil (imajiner)
Untuk lebih jelasnya, lihat video tutorial sifat-sifat akar persamaan kuadrat, klik disini
Rumus-rumus Akar Persamaan Kuadrat
Lihat penyelesaian persamaan kuadrat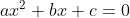 , yaitu:
, yaitu:
3. Untuk
Untuk lebih jelasnya, lihat video tutorial sifat-sifat akar persamaan kuadrat, klik disini
Rumus-rumus Akar Persamaan Kuadrat
Lihat penyelesaian persamaan kuadrat
atau dapat kita tuliskan sebagai:
Dari kedua penyelesaian di atas, jika kita jumlahkan dan kalikan akan diperoleh rumus-rumus akar, yaitu:
1)
2)
Contoh:
Diketahui persamaan kuadrat
1.
2.
3.
4.
Penyelesaian:
PK :
BU :
Sehingga
1.
2.
3.
4.
Untuk lebih jelasnya, lihat video tutorial rumus-rumus akar, klik disini
Menyusun Persamaan Kuadrat
Contoh 1
Persamaan kuadrat yang akar-akarnya 2 dan 3 adalah ....
Penyelesaian:
Contoh 2
Persamaan kuadrat yang akar-akarnya -1 dan 4 adalah ....
Penyelesaian:
Contoh 3
Persamaan kuadrat yang akar-akarnya 3 dan -5 adalah ....
Penyelesaian:
Dari ketiga contoh di atas, dapat diambil kesimpulan bahwa, persamaan kuadrat yang akar-akarnya 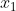 dan
dan 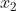 adalah:
adalah:
Contoh 4
Persamaan kuadrat
Penyelesaian:
PK :
BU :
(i) jumlahkan akar-akar PK yang diketahui:
(ìi) kalikan akar-akar PK yang diketahui:
Jadi persamaan kuadrat barunya adalah:
Untuk lebih jelasnya, lihat video tutorialnya di sini.

No comments:
Post a Comment